베이지안 추론
베이지안 추론과 관련한 몇 가지 개념을 짚고, 예시를 통해 추론 방법을 적용해보고자 합니다.
베이즈 정리 (Bayes’ Theorem): 베이즈 정리는 주어진 데이터 (\(D\))에 대한 파라미터 (\(\theta\))의 사후 확률 분포를 계산하는 공식입니다. 베이즈 정리는 다음과 같이 표현됩니다:
\[ p(\theta | D) = \frac{p(D | \theta) \pi(\theta)}{p(D)} \]
여기서:
- \(p(\theta | D)\) : 데이터 (\(D\))가 주어졌을 때 파라미터 (\(\theta\))의 사후 확률 (Posterior Probability)
- \(p(D | \theta)\) : 파라미터 (\(\theta\))가 주어졌을 때 데이터 (\(D\))가 나타날 확률 (우도, Likelihood)
- \(\pi(\theta)\) : 파라미터 (\(\theta\))의 사전 분포 (Prior Distribution)
- \(p(D)\) : 데이터 (\(D\))의 주변 분포 (Evidence, 증거)
사전 분포 (\(\pi(\theta)\), Prior Distribution): 파라미터 (\(\theta\))에 대한 초기 신념 또는 사전 지식입니다. 데이터가 수집되기 전에 우리가 파라미터 (\(\theta\))에 대해 갖고 있는 믿음을 나타냅니다.
우도 (Likelihood, \(p(D | \theta)\)): 주어진 파라미터 (\(\theta\)) 아래에서 데이터 (\(D\))가 나타날 확률입니다. 이는 모델의 파라미터가 주어졌을 때 데이터를 관찰할 확률 분포를 나타냅니다.
사후 분포 (Posterior Distribution, \(p(\theta | D)\)): 데이터 (\(D\))가 주어졌을 때 파라미터 (\(\theta\))의 갱신된 확률 분포입니다. 이는 사전 분포와 우도를 결합하여 계산됩니다.
증거 (Evidence, \(p(D)\)): 데이터 (\(D\)) 자체의 확률로, 이는 사전 분포와 우도의 결합을 통해 계산됩니다. 증거는 모든 가능한 파라미터 (\(\theta\))에 대해 데이터를 관찰할 확률의 총합입니다:
\[ p(D) = \int p(D | \theta) \pi(\theta) d\theta \]
앞면이 나올 확률 \(\theta\)를 추정하고자 합니다. 우리는 \(\theta\)에 대한 사전 확률 분포로 베타 분포를 사용하고, 관찰된 데이터 \(D\)는 베르누이 분포를 따릅니다.
사전 분포
사전 분포는 베타 분포로 설정합니다:
\[ \theta \sim \text{Beta}(\alpha, \beta) \]
여기서 \(\alpha\)와 \(\beta\)는 베타 분포의 모수입니다. 베타 분포의 확률 밀도 함수는 다음과 같습니다:
\[ \pi(\theta) = \frac{\theta^{\alpha-1} (1 - \theta)^{\beta-1}}{B(\alpha, \beta)} \]
우도
우도는 베르누이 분포로 설정합니다. 데이터 \(D\)는 \(n\)번의 독립적인 실험에서 \(x\)번의 성공(앞면)을 관찰한 결과라고 가정합니다:
\[ D = (x_1, x_2, \ldots, x_n) \]
각 \(x_i\)는 베르누이 분포를 따릅니다:
\[ x_i \sim \text{Bernoulli}(\theta) \]
베르누이 분포의 확률 질량 함수는 다음과 같습니다:
\[ p(x_i | \theta) = \theta^{x_i} (1 - \theta)^{1 - x_i} \]
따라서 전체 데이터 \(D\)에 대한 우도는 다음과 같습니다:
\[ p(D | \theta) = \theta^x (1 - \theta)^{n - x} \]
여기서 \(x\)는 \(D\)에서 성공(앞면)의 총합입니다.
사후 분포
사후 분포는 베이즈 정리를 사용하여 계산합니다:
\[ p(\theta | D) = \frac{p(D | \theta) \pi(\theta)}{p(D)} \]
이는 다음과 같이 다음과 같이 \(p(\theta | D)\) 가 \(p(D | \theta) \pi(\theta)\)에 비례한다고 쓸 수 있습니다:
\[ p(\theta | D) \propto p(D | \theta) \pi(\theta) \]
증거 \(p(D)\)는 모든 \(\theta\)에 대해 데이터 \(D\)의 우도와 사전 분포를 결합한 것입니다:
\[ p(D) = \int_0^1 p(D | \theta) \pi(\theta) d\theta \]
베타 분포와 베르누이 분포의 특성으로 인해, 사후 분포 역시 베타 분포가 됩니다. 즉, 사후 분포는 다음과 같습니다:
\[ \theta | D \sim \text{Beta}(\alpha + x, \beta + n - x) \]
예시
동전을 던져 앞면이 나오면 1, 뒷면이 나오면 0을 기록했다고 하겠습니다. 총 10번을 던져 기록한 데이터는 다음과 같습니다:
\[ x_1, x_2, \ldots, x_{10} = 1, 1, 0, 0, 0, 0, 1, 0, 0, 0 \]
이 데이터를 바탕으로 사후 분포를 계산하기 위해 필요한 단계는 다음과 같습니다.
단계 1: 사전 분포 설정
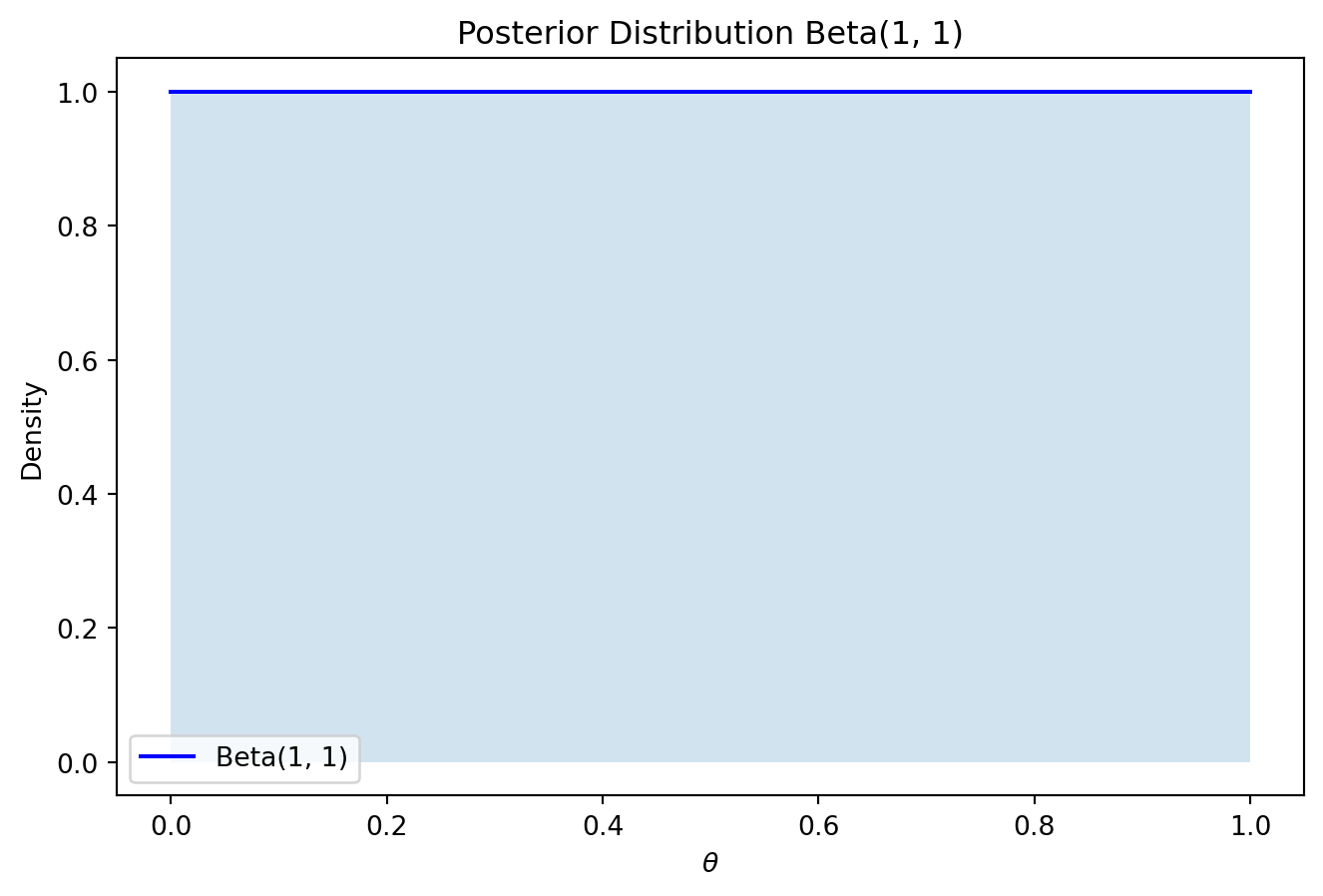
사전 분포는 베타 분포로 설정합니다. 예를 들어, \(\alpha = 1\)과 \(\beta = 1\)을 선택하여 무정보 사전분포 (uniform prior)를 사용한다고 가정합니다. 이는 \(\theta \sim \text{Beta}(1, 1)\)를 의미합니다.
\(\text{Beta}(1, 1)\)은 다음과 같은 모습입니다.
단계 2: 우도 계산
우도는 베르누이 분포로 설정합니다. 주어진 데이터에서 성공(1)의 횟수 \(x\)와 실패(0)의 횟수를 구합니다. 주어진 데이터에서 성공 횟수 \(x\)는 다음과 같습니다:
\[ x = 1 + 1 + 0 + 0 + 0 + 0 + 1 + 0 + 0 + 0 = 3 \]
실패 횟수는 \(n - x = 10 - 3 = 7\)입니다.
단계 3: 사후 분포 계산
사후 분포는 사전 분포와 우도를 결합하여 계산합니다. 사후 분포는 다음과 같이 베타 분포가 됩니다:
\[ \theta | D \sim \text{Beta}(\alpha + x, \beta + n - x) \]
여기서:
- \(\alpha = 1\)
- \(\beta = 1\)
- \(x = 3\)
- \(n - x = 7\)
따라서, 사후 분포는 다음과 같습니다:
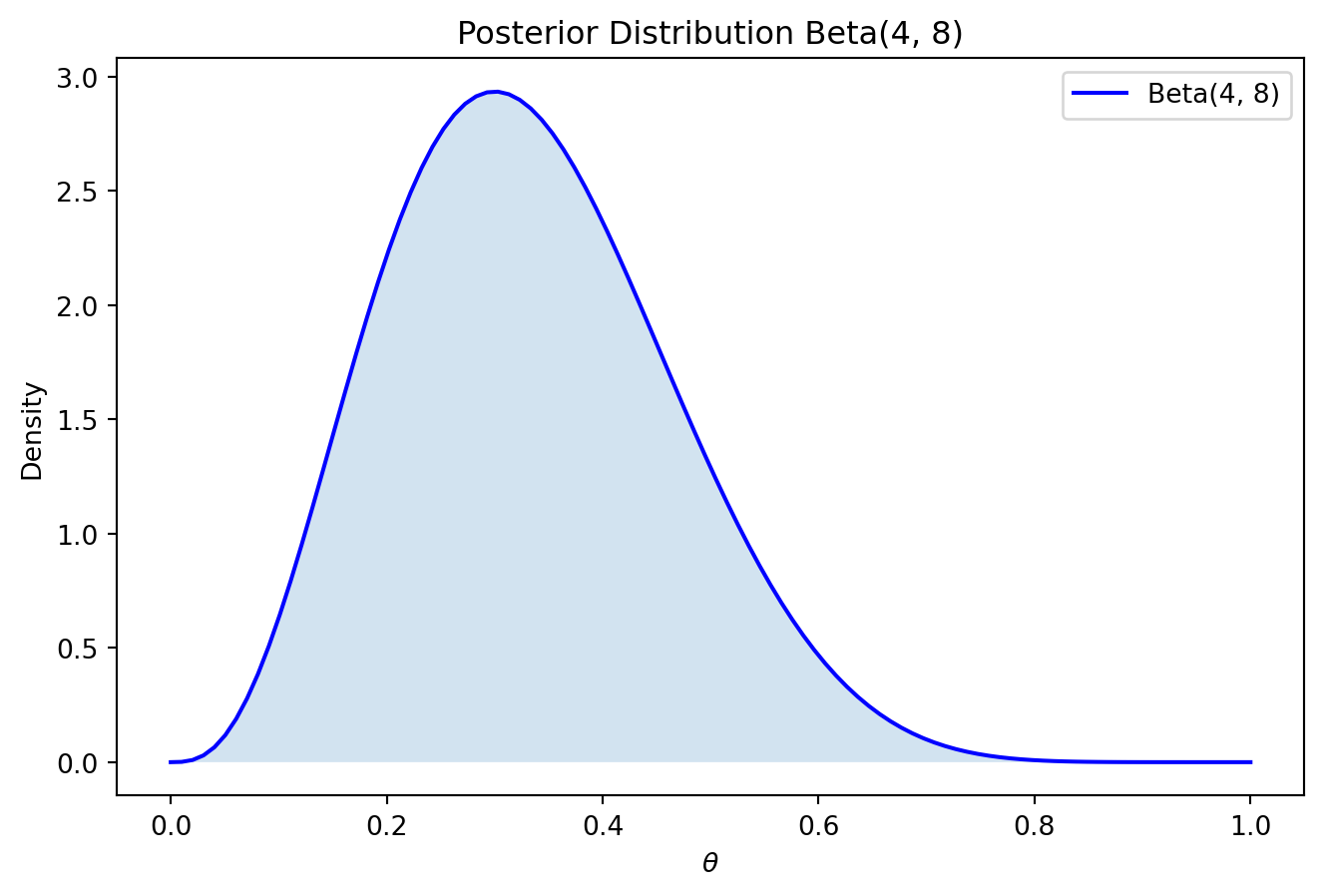
\[ \theta | D \sim \text{Beta}(1 + 3, 1 + 7) = \text{Beta}(4, 8) \]
결과
주어진 데이터에 기반한 사후 분포는 \(\text{Beta}(4, 8)\)입니다. 이 분포는 \(\theta\)에 대한 우리의 갱신된 믿음을 나타내며, 새로운 데이터가 주어지면 이 분포를 다시 업데이트할 수 있습니다.